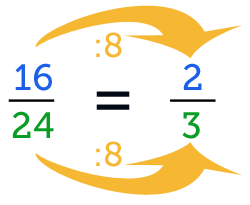Brüche Kürzen
Was ist das Kürzen eines Bruchs
Für jeden Bruch gibt es eine einfachste Form. Die einfachste Form ist ein Bruch, bei dem der Zähler (die obere Zahl) und der Nenner (die untere Zahl) so klein wie möglich sind. Um Brüche zu kürzen, muss der Bruch so klein wie möglich gemacht werden.
Ein Beispiel für das Kürzen eines Bruchs: 36 12
Sind die hier beschriebenen Begriffe schwierig? Sieh dir die 'Was ist ein Bruch?' Seite an, um zuerst weitere Erklärungen zu erhalten.
Auf dieser Seite findest du Beispiele und Übungen. Gehe zu einem der 5-Schritte-Pläne, um ausgiebig zu üben.
5-Schritte-Pläne
Wie kürzt man einen Bruch?
Um einen Bruch zu kürzen, suchst du nach dem größten gemeinsamen Teiler (ggT). Mit dem größten gemeinsamen Teiler meinen wir die höchste Zahl, durch die du sowohl den Zähler als auch den Nenner teilen kannst. Dann musst du den Zähler und den Nenner durch diese Zahl teilen, um den Bruch so einfach wie möglich zu machen.
Unten findest du Beispiele mit Erklärungen und Übungen
Beispiel 1
Wir werden den Bruch 24 kürzen.
24 ZählerNenner
Was ist der größte gemeinsame Teiler von 24?
Der Zähler ist 2 und du kannst ihn nur durch 1 und 2 teilen.
Der Nenner ist 4 und du kannst ihn durch 1, 2, und 4 teilen.
Dann musst du nach der höchsten Zahl suchen, durch die du beide teilen kannst. Das ist 2, also ist der größte gemeinsame Teiler 2.
2(Zähler) geteilt durch 2 ist 1. 4(Nenner) geteilt durch 2 ist 2. So erhältst du den gekürzten Bruch 12.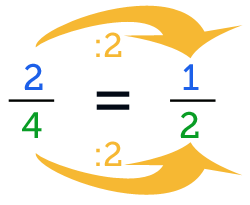
Übung 1:
Kürze den Bruch. Die Nenner sind bereits eingegeben. Wähle die Anzahl der Rechnungen und die Zeit pro Rechnung und klicke auf Start.
Tipp: Verwende die Tab-Taste, um zum nächsten Feld zu gelangen
Übung 2:
Kürze den Bruch. Wähle die Anzahl der Rechnungen und die Zeit pro Rechnung und klicke auf Start.
Tipp: Verwende die Tab-Taste, um zum nächsten Feld zu gelangen
Beispiel 2
Wir werden jetzt den Bruch 68 kürzen.
Als erstes suchen wir den größten gemeinsamen Nenner.
Der Zähler ist 6, dieser kann durch 2,3 und 6 geteilt werden.
Der Nenner ist 8, dieser kann durch 2,4 und 8 geteilt werden.
Der größte gemeinsame Teiler für 68 ist 2. Dies ergibt den gekürzten Bruch 34.
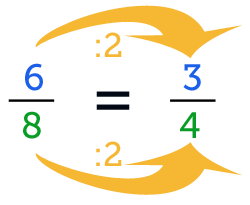
Beispiel 3
Wir werden jetzt den Bruch 1624 kürzen.
16(Zähler) kann geteilt werden durch: 2, 4, 8 und 16.
24(Nenner) kann geteilt werden durch: 2,3, 4, 6, 8, 12 und 24.
Der größte gemeinsame Teiler für 1624 ist 8. 16 geteilt durch 8 ist 2 und 24 geteilt durch 8 ist 3.
Dies ergibt den gekürzten Bruch 23.
